なぜ出力は速度の三乗に比例するのか導いてみた
目次
記事の目的
力は速度の2乗，出力は速度の3乗に比例すると言われている。
本記事では出力は速度の3乗に比例することを水力発電の理論出力式とベルヌーイの定理から導出した。
英語版の記事は以下よりアクセス可能です。
⇒⇒⇒https://lifeisfruits.com/2020/03/11/why-output-is-proportional-to-velocity-cubed_en/
導出するにあたって
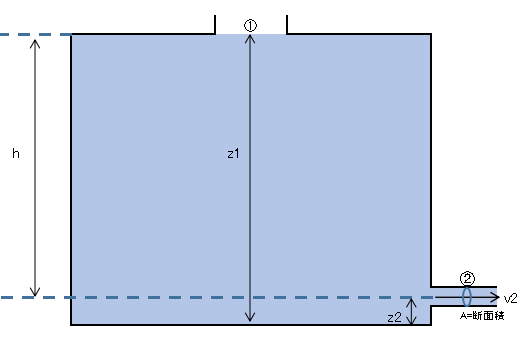
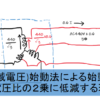
導出するにあたって図の通り水を貯めているタンクのモデルケースで考える。
地点➀はタンクに水が溜めた水面の地点であり，地点➁は水の排出口である。
なお，数式にて使用する変数の定義は一番最後の項目にて補足する。
排出口における理論出力について
最初に排出口の地点➁における理論出力の式について考える。
数式は以下の通り定義される。
$$P_{out}=9.8Q(z_1-z_2)ρ$$
$$P_{out}=9.8Q(h)ρ$$
水の密度ρはおよそ$${1ton/m}^3$$であることから
$$P_{out}=9.8Qh$$となる。
また、流量Qは排出口の断面積Aと流体の速度vから以下の関係式で表せる。
$$Q=Av_2$$
よって、以下の通り数式展開される。
$$P_{out}=9.8Av_2h{…数式1}$$
ベルヌーイの定理を適用する
次にベルヌーイの定理をモデルケースに適用すると次の関係式を導くことが出来る。
$$\frac{1}{2}v_1^2+\frac{P_1}{ρ}+gz_1=\frac{1}{2}v_2^2+\frac{P_2}{ρ}+gz_2$$
ここで第二項における圧力は両点とも大気圧だから省略が可能である。
また，地点1は速度がゼロあり，地点2は高さの基準となることから以下の関係式が導かれる。
$$g(z_1-z_2)=\frac{1}{2}v_2^2$$
$$gh=\frac{1}{2}v_2^2$$
$$h=\frac{v_2^2}{2g}{…数式2}$$
出力は速度の3乗に比例することを水力発電の理論出力式とベルヌーイの定理から導く
最後に数式1に数式2を代入することで数式3が算出され，出力は速度の三乗に比例することが分かる。
$$P_{out}=9.8Av_2h{…数式1}$$
$$P_{out}=9.8\frac{Av_2^3}{2g}{…数式3}$$
[補足]数式に使用する変数の定義と単位の関係
Pout[kW]:排出口(地点➁)における理論出力
z1[m]：水面（地点➀）におけるタンク底からの距離
v1[m/sec]：水面（地点➀）における流体の速度
P1[Pa or N/m2]：水面（地点➀）における流体の圧力
z2[m]：排出口(地点➁)におけるタンク底からの距離
v2[m/sec]：排出口(地点➁)における流体の速度
P2[Pa or N/m2]：排出口(地点➁)における流体の圧力
ρ[ton/m3]：水の密度
Q[m3/sec]：排出口(地点➁)における流量
h[m]：地点➀から地点➁までの高さ方向の距離
A[m2]:排出口の断面積
g[m2/sec]：重力加速度