【電験三種】三相有効電力の公式 P=Vs・Vr・sinδ/Xを導くには
目的
この記事では電験三種の過去問（平成21年電力の問7）にて出題された交流三相3線式1回線の送電線路における受電端負荷の三相有効電力[W]がなぜ，Vs・Vr・sinδ/Xにて表されるのか，導出する過程を示す。
公式を丸暗記するのではなく，導出の過程に興味のある方の参考になれば幸いである。
電験三種 平成21年電力の問7の問題
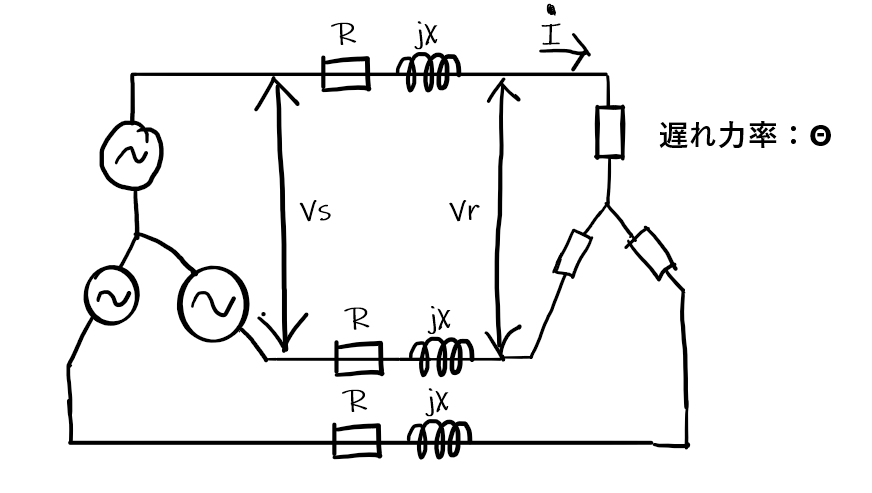
交流三相3線式1回線の送電線路があり，受電端に遅れ力率角Θ[rad]の負荷が接続されている。送電端の線間電圧をVs[V]，受電端の線間電圧をVr[V]，その間の位相角はσ[rad]である。受電端の負荷に供給されている三相有効電力[W]を表す式として，正しいのは次のうちどれか。
ただし，送電端と受電端の間における電線1線当たりの誘導性リアクタンスはX[Ω]とし，線路の抵抗，静電容量は無視するものとする。
解答
P=\frac{Vs\sin \delta}{X}Vr
導出過程
公式を暗記していれば速攻で解答が可能な問題となるが，以降に示す手順を踏めば公式を暗記せずとも解答可能である。
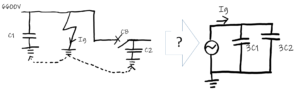
まず，イメージアップのため問題文が意図する平衡三相回路を描く。
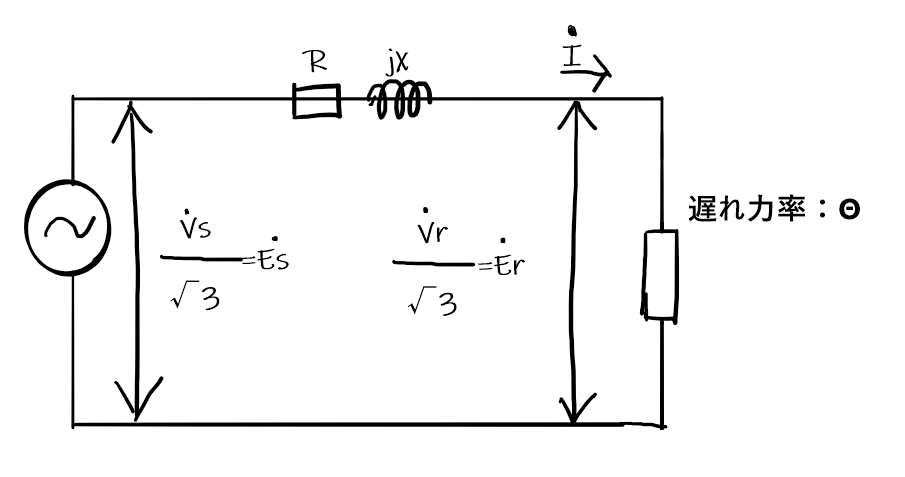
この回路を単相回路に変換を行う。
さて，ここから問われている受電端の有効電力の公式を導出していく。公式は下記2つの数式より求めることが可能となる。
数式➀：三相負荷の皮相電力を求める公式。受電端電圧（共役複素数）と負荷電流を乗じ，更に相数3を乗ずる。
S=3\overline{E}r I=P±jQ
数式➁：単相回路におけるベクトル図より送電端電圧は受電端電圧，負荷電流，送電端電圧及び送電線路のインピーダンスにて以下の関係式で表せる。
Es=Er+RI+jXI
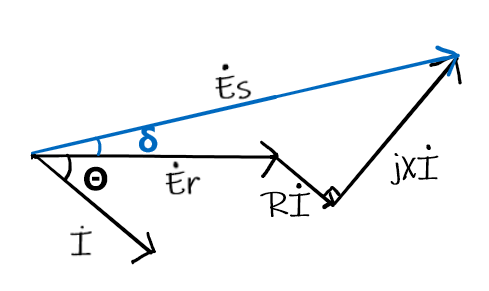
「ベクトル図」
まず，数式➁を変形するとIは次の通り求められる。
I=\frac{Es-Er}{R+jX}
次にErのベクトルを基準とした際，Esを複素数で表現し直すと次式となる。I=\frac{Es\cos \delta +jEs\sin \delta -Er}{R+jX}
また，問題では線路の抵抗は無視させることから分母のRは省略される。
I=\frac{Es\cos \delta +jEs\sin \delta -Er}{jX}
分母が虚数であることから，分母及び分子に-jを乗じて有理化しする。また，分子は実数部と虚数部とに整理する。
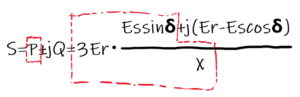
I=\frac{Es\sin \delta +j(Er-Es\cos \delta )}{X}
得られた結果を数式➀に代入する。問題では有効電力Pについて問われているので，実数部のみを着目する。
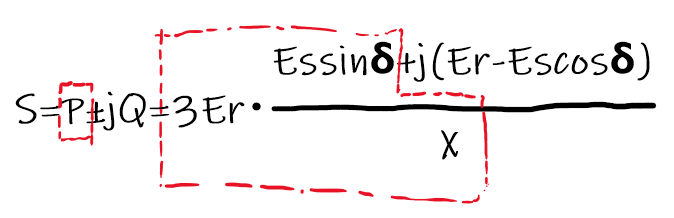
P=3\frac{Es\sin \delta}{X}Er
仕上げに相電圧と線間電圧は以下の関係があったのでそれぞれ代入する。
Es=\frac{Vs}{\sqrt{3}}
Er=\frac{Vr}{\sqrt{3}}
以上で受電端負荷における有効電力Pは次式にて求められることが分かる。
P=\frac{Vs\sin \delta}{X}Vr