水盛りの計測原理と計測手順（水平時/傾斜時)
水盛りとは
透明なゴムホースの中に水を入れ，両端の水面高さが同じとなる事象を利用して，物の高さを計測したり水平を確認するものである。
ゴムホース中に入れる水には，気泡が含まれないことを注意する必要がある。
水盛りの計測原理
下記図に水盛りのイメージ図を示す。
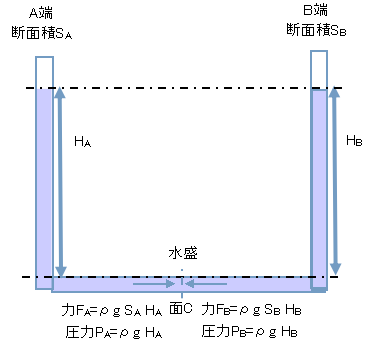
水盛りに1種類の液体を入れると，各容器の液面の高さは，容器の管の太さや形にかかわりなくすべて同じになる
この事象は，下記に示すパスカルの原理にて説明される。
・静止流体の中の面に働く応力は，その面に垂直な圧力だけで，面に沿う方向のずれ応力は働かない。
・流体内の任意の1点における圧力は，すべての方向に対して等しい。
数式で表したものが静水圧の式であり，P=ρghにて示される。
（P:静水圧[N/m^2]， g:重力加速度[m/s^2] ， h:高さ[m]）
たとえば，上図のケースだと，底面Aにかかる圧力PAは、PA=ρgHAとなり，底面Bにかかる圧力PBは、PB=ρgHBであらわせる。
A端とB端をつなぐ配管における面Cでの左右の圧力は同じであるから，PA＝PBでなければならないため，結果的にHA＝HBとなり，両端の水面が同じ高さになる。
水平な場所における水盛りを使用した計測の一例
水盛りを使用した計測例を紹介する。
下図のように水平な地盤があり，A端側には既知の高さの物体が設置されている。
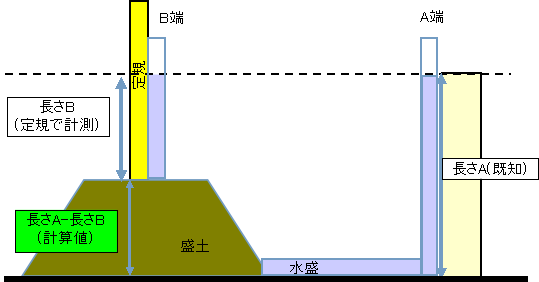
B端側は盛土がされており，盛土の高さを求める際に水盛りを使用するのに踏む手順は以下の通りである。。
①盛土した上面から水盛りB端の水面までの長さBを定規で計測する。
②水盛りの水面高さはA端，B端同じであることから，盛土の高さは，
盛土の高さ＝長さA-長さB
にて算出することが出来る。
傾斜がある場所において水盛り計測した際の計測の一例
3項では水平な場所における計測を示したが，本項では下図のように傾斜θがある場所における計測例を紹介する。
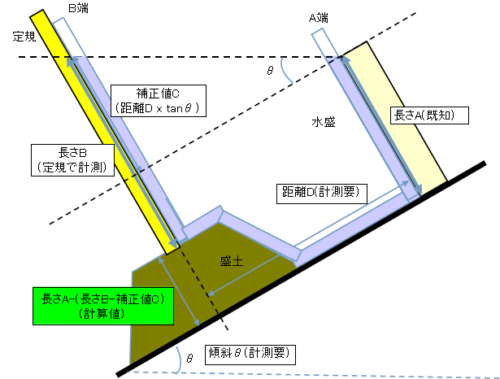
本計測では3項にて計測した長さBに加えて，
I 水盛りA端，B端間の距離 距離D
II 地盤が傾いている傾斜θ
の二つを計測し，補正値Cを加味して求める必要がある。
このケースにおける盛土の高さは，
盛土の高さ＝長さA-(長さB-補正値C)
＝長さA-(長さB-距離D x tanθ）
にて求めることが出来る。