[丸暗記不要]ベルヌーイの定理の数式を導く方法
記事の目的
ベルヌーイの定理の数式は以下の通りである。
$$\frac{1}{2}v_1^2+\frac{P_1}{ρ}+gz_1=\frac{1}{2}v_2^2+\frac{P_2}{ρ}+gz_2={const}$$
いささか数式が長く,習う時期が大学以降であることから,真剣に勉強し,自分の頭にしっかり刻むことが出来た方は少ないのではないか。
この記事を読めば,高校で習った知識を活用することで,ベルヌーイの数式を導くことが出来るようになる。
覚えることに苦手意識がある方の参考になれば幸いである。
ベルヌーイの数式とは
完全流体の定常流れにおいて、流線上でエネルギーが保存されることを示した定理である。完全流体とは粘性のまったくない仮想的な流体を意味する。
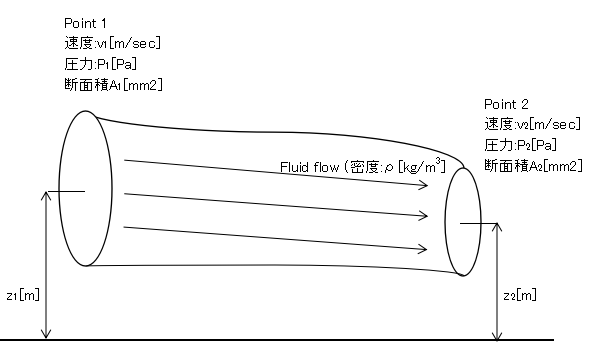
以下の図の通りPoint1及びPoint2における流体の状態を変数で表すと,以下の式で表される。また,重力加速度はg[m/s2]とする。
$$\frac{1}{2}v_1^2+\frac{P_1}{ρ}+gz_1=\frac{1}{2}v_2^2+\frac{P_2}{ρ}+gz_2={const}$$
ベルヌーイの数式を導く(その1)
ベルヌーイの数式は以下の3つのエネルギー量の総和である。
1. 運動エネルギー
2. 圧力エネルギー
3. 位置エネルギー
高校物理を習得していれば1.運動エネルギー,3.位置エネルギーはエネルギー保存則で馴染みのあるものであろう。
2.圧力エネルギーは少しピンとこないかもしれないが,一つずつ式展開をしていけば,これも十分理解できるものである。
運動エネルギーとは
まずは運動エネルギーについて述べる。
質量m[kg]の物体が速度v[m/s]で移動しているときの運動エネルギーPoutk[J]は
$${Poutk}=\frac{1}{2}mv^2$$
にて表すことが出来る。この数式は高校物理でよく登場したものだ。
流体にこのケースにあてはめると,質量mを流速v[m/sec],断面積A[m2]及び密度ρ[kg/m3]で表現すれば良く,単位時間あたりの運動エネルギーPout_k[J/sec]は
$${Poutk}=\frac{1}{2}vAρv^2$$
で表すことが出来る。
圧力エネルギーとは
次に圧力エネルギーについて述べる。
この圧力という考え方に馴染みのある方が多くないのではないだろか。
もし,時間があれば以下の記事にて圧力に対する説明をしているので時間の許す方はご参照ください。
圧力P[Pa]とは単位面積に対する力の単位であることから,力F[N]が断面積A[m2]にかかることを想定すると
$${P}=\frac{F}{A}$$
で表すことが出来る。
また,とある物体に対して力F[N]をかけた際に,その物体が1秒でどれだけの距離動かせたか(速度v[m/sec])を乗することで単位時間あたりのエネルギーPoutpress[J/sec]を求めることが出来る。
$${Poutpress}=Fv$$
よって単位時間あたりのエネルギーを圧力を用いて表すには以下の数式展開にて得られる。
$${Poutpress}=PAv$$
位置エネルギーとは
最後に位置エネルギーPoutpotは,質量m[kg]の物体が重力加速度g[m/s2]の中,高さz[m]に位置しているときは以下の数式で表すことが出来る。
$${Poutpot}=mgz$$
この数式も高校物理でよく登場したものだ。
前述の運動エネルギーで述べた通り,質量mは流速v[m/sec],断面積A[m2]及び密度ρ[kg/m3]で表現すれば良く単位当たり時間の位置エネルギーPoutpot[J/sec]は
$${Poutpot}= Avρgz$$
となる。
ベルヌーイの数式を導く(その2)
流体中における運動エネルギー,圧力エネルギー,位置エネルギーの総和は
$$Poutk + Poutpress + Poutpot$$
である。
前述の通り流体中で表現すると以下の通りとなり,数式展開することでベルヌーイの数式が得られる。
$$Poutk + Poutpress + Poutpot$$
$$=\frac{1}{2}vAρv^2+PAv+Avρgz$$
$$=\frac{1}{2}v^2+\frac{P}{ρ}+gz$$
ベルヌ―イの数式を扱う情報源によっては,上記の数式の全項に対して密度ρを乗したり,高さ変数zを除するケースもみられるが,そもそもこの数式はエネルギー保存の法則を示したものなので何ら問題はない。





















ディスカッション
コメント一覧
まだ、コメントがありません