交流回路の電圧降下計算式”RIcosθ+XIsinθ”を導出するには
目的
電気設備では送電端（配電盤や給電盤）からケーブルを介して，負荷に対して交流電力を供給しているため，ケーブルが有するインピーダンス（抵抗及びリアクタンス）により電圧降下が発生する。
このことから，受電端が規則や負荷が必要な電圧となるようケーブルサイズの検討が必須である。
本記事では，ケーブルサイズの検討の一環として使用する交流電源による電圧降下の公式”RIcosθ+XIsinθ"を導出するまでの過程について纏める。
送電端からケーブルを介し負荷に給電する回路図を描く
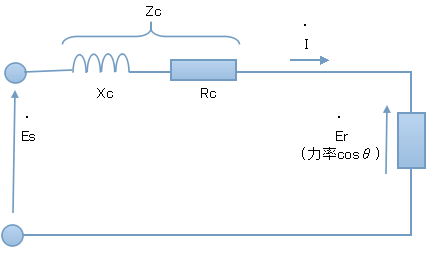
送電端からケーブルを介し負荷に給電している回路図は以下の通り描ける。なお，回路中における変数は以下の通り定義される。
Es：送電端となる交流電圧[V]
Er：受電端となる交流電圧[V]
I：回路中に流れる電流[A]
cosθ：受電端に接続される負荷の力率
Rc：送電端から受電端までのケーブルの抵抗[Ω]
Xc：送電端から受電端までのケーブルのリアクタンス[Ω]
回路図からベクトル図をステップ毎に描く
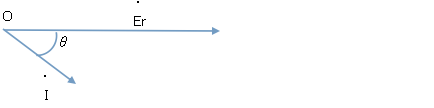
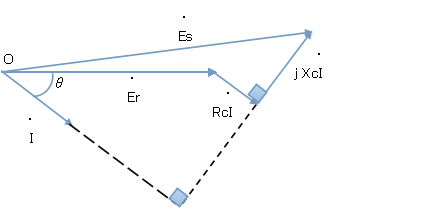
1．ゼロ点Oからベクトル図の基準となる受電端Erを描き，負荷（力率cosθ)に流れる電流IをErよりθだけ遅らせて描く
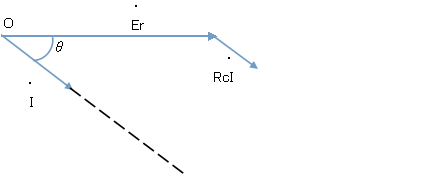
2．ケーブルの抵抗による電圧降下分RcIを受電端Erの先に描く。抵抗による電圧降下は電流に対し同位相であるため，電流Iに対し平行に描く。また，下準備として電流Iを延長した線を補助線として描く。
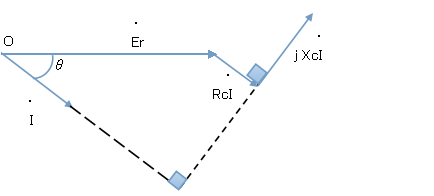
3. ケーブルのインダクタンスによる電圧降下分XcIをRcIの先から描く。インダクタンスによる電圧降下は電流に対し90°進むように描く。
4.ゼロ点Oから電圧降下分XcIの先端を結んだものが送電端電圧Esのベクトルとなる。
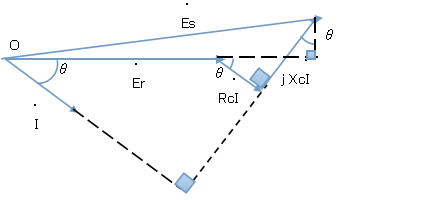
5.次の下準備として受電端電圧Erを延長した補助線 及び その補助線に対する送電端電圧Esからの垂線を描く。
6. ケーブルの抵抗及びリアクタンスによる電圧降下のベクトルは，水平成分と垂直成分で表現でき，①～④のように示すことが出来る。
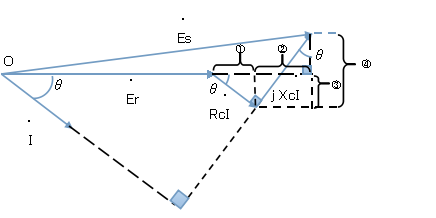
$$\scriptsize{①:}{RcI}\cos\theta{, }\scriptsize{②:} {XcI}\sin\theta{, }
\scriptsize{③:} {RcI}\sin\theta{, }\scriptsize{④:} {XcI}\cos\theta$$
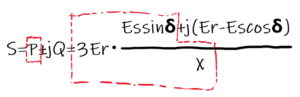
7. 6項に示す図の通り，三平方の定理を利用すると送電端電圧Esは以下の数式で示すことが出来る。
$$\scriptsize{Es=}\sqrt{({Er}+{RcI}\cos\theta+{XcI}\sin\theta)^2+({XcI}\cos\theta-{RcI}\sin\theta)^2}$$
また，上記数式の第一項と第二項を比較すると第二項の
$$\scriptsize({XcI}\cos\theta-{RcI}\sin\theta)^2$$
は，第一項の
$$\scriptsize({Er}+{RcI}\cos\theta+{XcI}\sin\theta)^2$$
と比べて非常に小さいことから，第二項が無視されることとなり，以下の数式に近似される。
$$\scriptsize{Es=}{Er}+{RcI}\cos\theta+{XcI}\sin\theta$$
電圧降下は，送電端電圧Esから受電端電圧Erを引くことより求めることが出来るので，以下の数式で求められる。
$$\scriptsize{ΔV=}{RcI}\cos\theta+{XcI}\sin\theta$$