不平衡負荷の電力計算。単純に接続負荷の消費電力の合計で良いのか？
’21/9/9 コメントにてご指摘頂いた点を訂正しました
記事の目的
単相電源における消費電力は，接続する負荷の電力を積み上げれば，算出できるのは納得いく。しかしながら，三相電源に不平衡負荷を接続した際には，負荷の電力の合計値が消費電力となるのであろうか。
エネルギー保存の法則から考えれば，単相・三相に限らず負荷で消費された電力を積み上げしたものが，消費電力となるはずである。
しかしながら，本当にそうなのかと少し疑問に感じるところがある。
この記事では三相不平衡負荷のケースを例に取り，実際に計算することで三相不平衡回路でも単純に負荷の電力消費量の積み上げが，その電力系統における消費電力であることを示す。
三相不平衡回路のモデルケースの設定
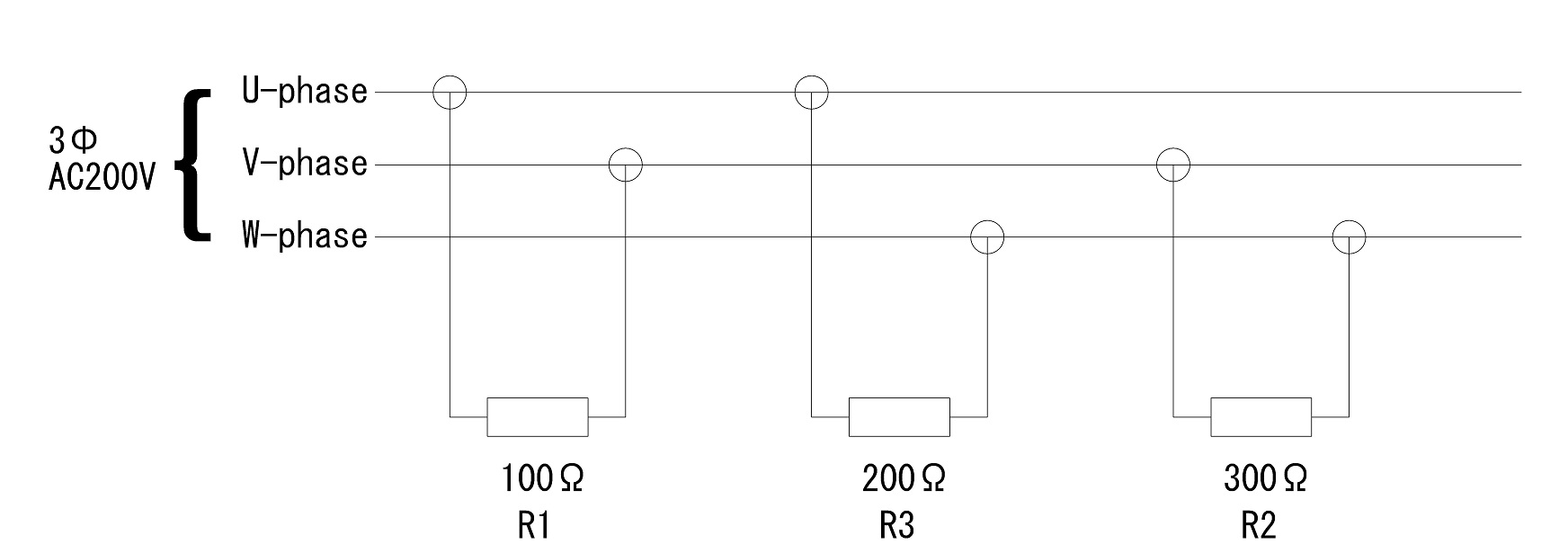
以下に示す通り三相200V電源にR1:100Ω，R2:300Ω，R3：200Ωを接続したケースを三相不平衡回路のモデルとして考える。
抵抗で消費される電力は，P=V2/Rで計算できるため，各負荷の消費電力は以下の通りとなる。
R1:400[W]
R2:133[W]
R3:200[W]
単純に電力積み上げすると733[W]である。
次項にて三相不平衡回路における各相に対する電流値を算出し，各相で消費される電力を算出し，単純に合計した値と一致するのか否かを検証する。
不平衡負荷の電力計算。単純に接続負荷の消費電力の合計で良いのか？
不平衡負荷の回路を解く方法は，日本電気技術者協会のサイトに掲載されている解法を参照した。この解法は以下がキーポイントとなる。
➀電源側の中性点と不平衡負荷の中性点間には一定の電位差が生じる。
➁負荷側において各相に流れる電流値の合計はゼロとなる。
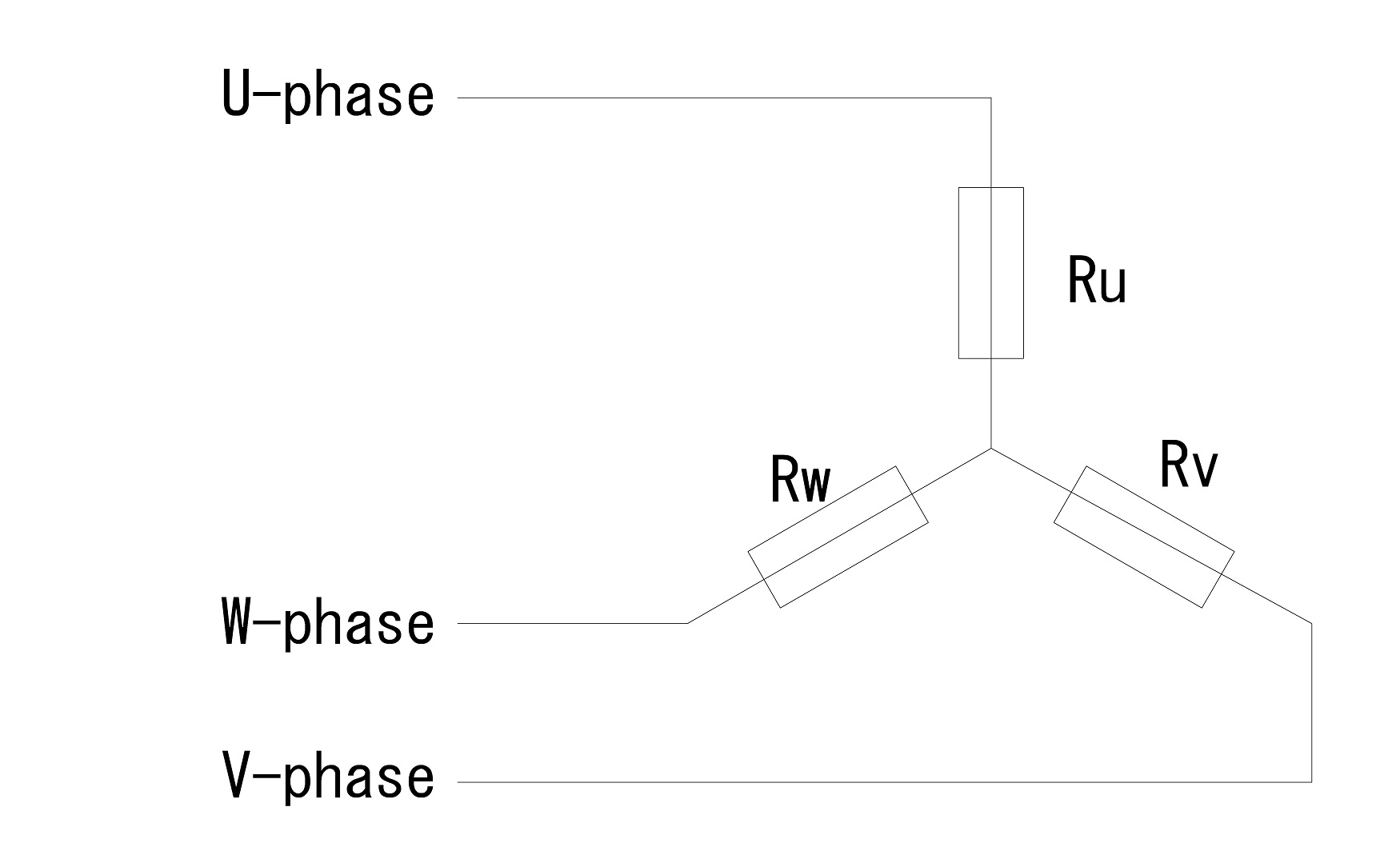
まず，モデルケースの負荷側回路は，以下の通りΔ結線である。
この回路には中性点が存在しないことから，ΔY変換によって中性点の有る回路に変換する。変換式は以下の通りとなる。
$${Ru}=\frac{R1R3}{R1+R2+R3}=33.3$$
$${Rv}=\frac{R1R2}{R1+R2+R3}=50$$
$${Rw}=\frac{R2R3}{R1+R2+R3}=100$$
電源側も中性点があるY結線の回路で構成する。この際，線間電圧が200Vとなるので，電源側の相電圧は200V/√3となるので注意が必要である。Y結線の電源側と負荷側の回路は以下の通り表現することが出来る。
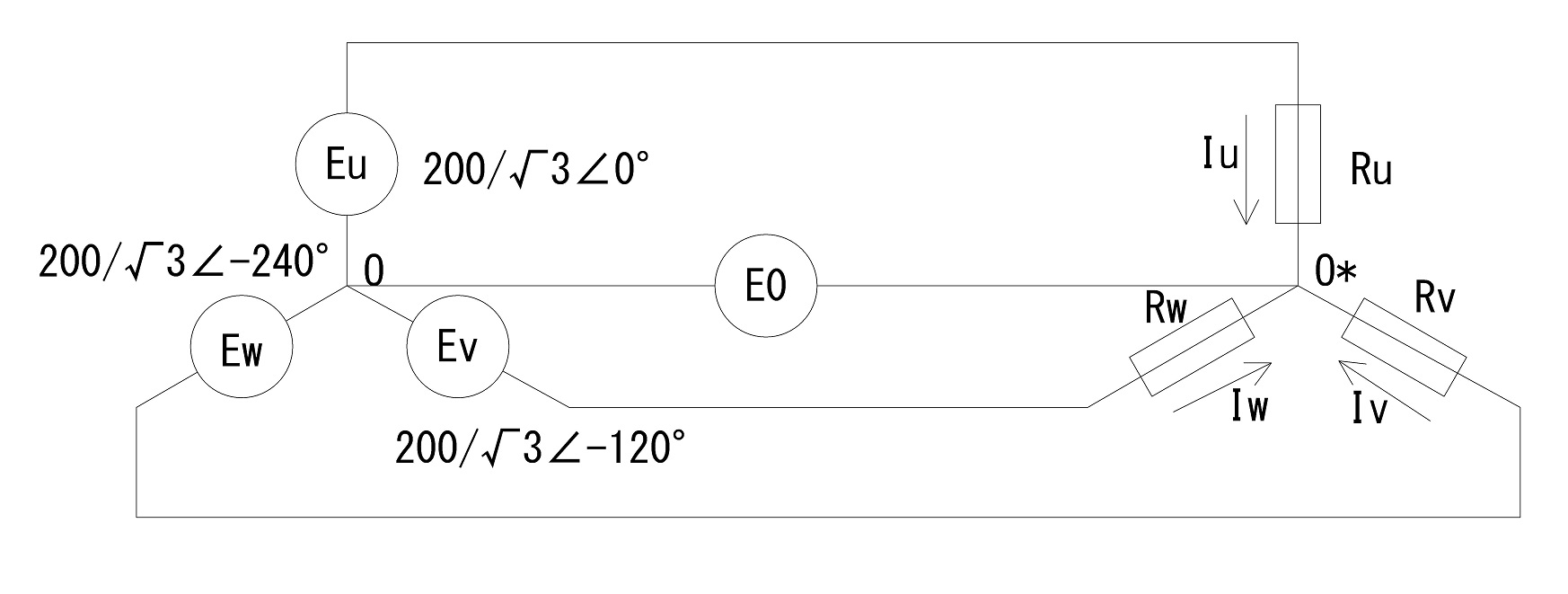
不平衡負荷を解く上で前述したキーポイント➁を適用すると，電源側と負荷側の中性点を結び一定電位差を設けることで以下の通り表現することが出来る。
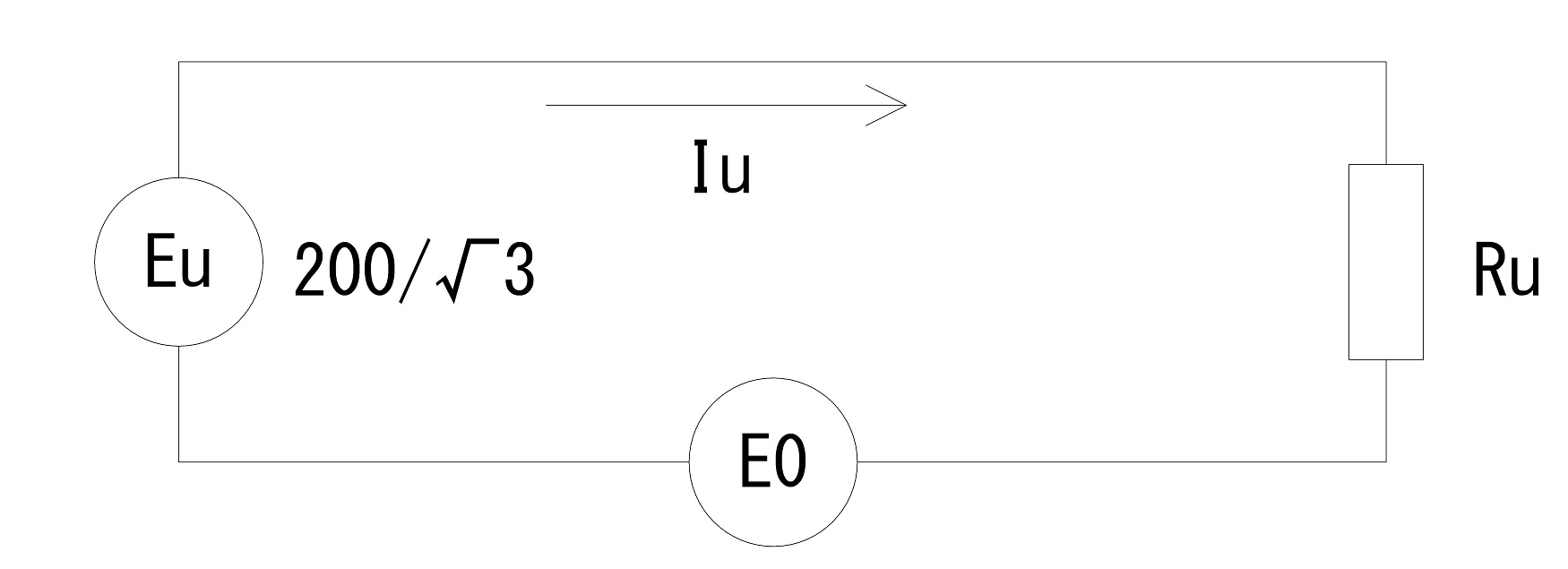
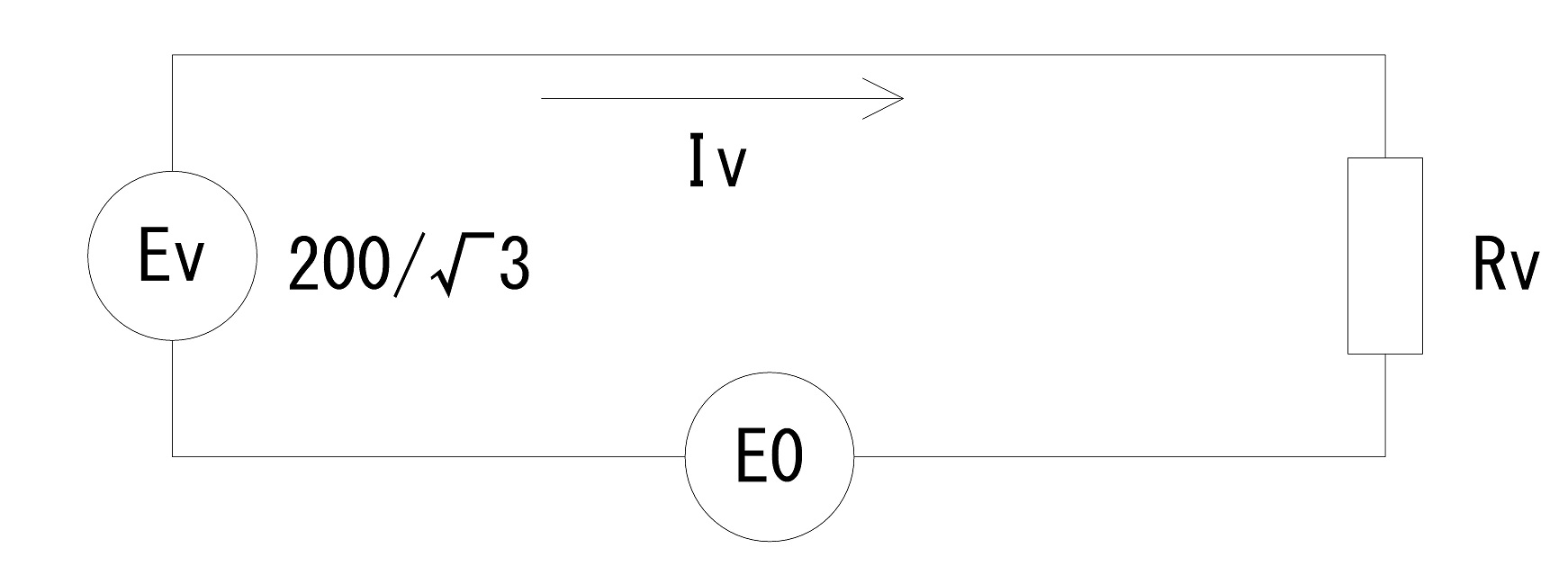
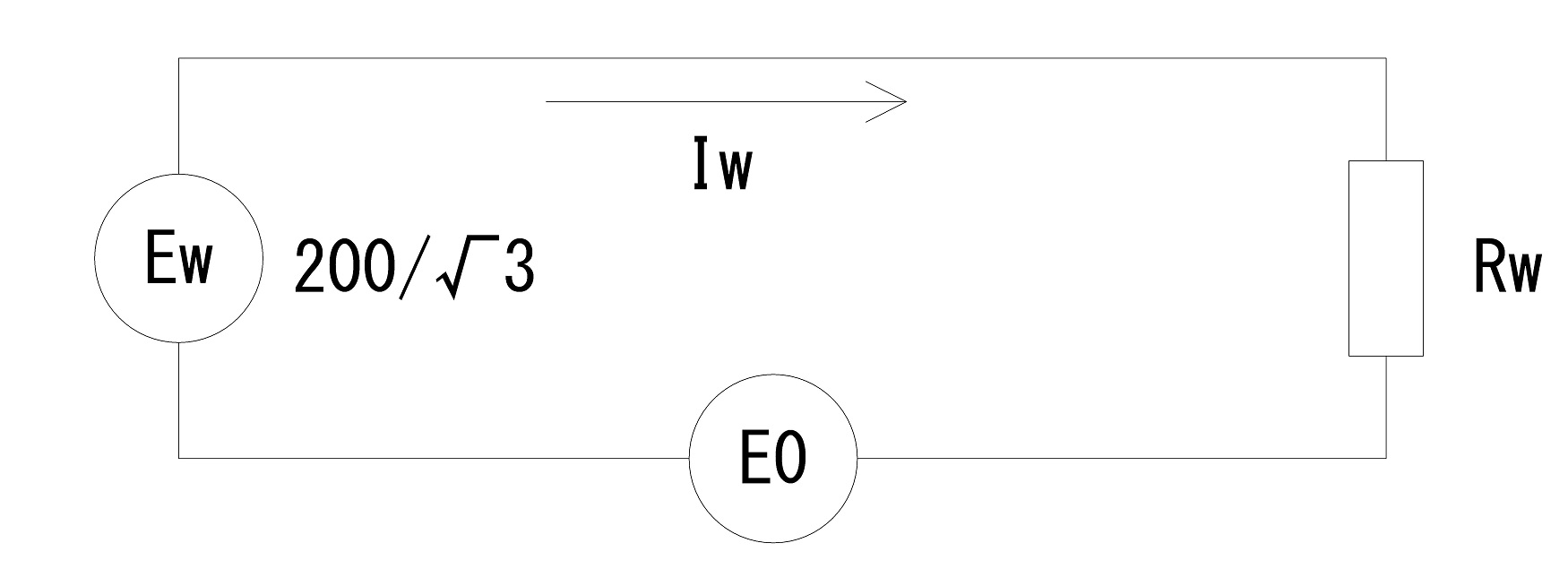
次に計算が容易になるよう，各相に分解した回路を示す。また，各相に流れる電流の算出式も併せて示す。
$${Iu}=\frac{Eu-Eo}{Ru}$$
$${Iv}=\frac{Ev-Eo}{Rv}$$
$${Iw}=\frac{Ew-Eo}{Rw}$$
前述したキーポイント➀を適用すると，各相の電流値の合計はゼロとなるため以下の数式で表現出来る。展開することで電源と負荷の中性点の電位差を求めることが出来る。
$${Iu}+{Iv}+{Iw}=0$$
$$\frac{Eu-Eo}{Ru}+\frac{Ev-Eo}{Rv}+\frac{Ew-Eo}{Rw}=0$$
$$\frac{Eu}{Ru}+\frac{Ev}{Rv}+\frac{Ew}{Rw}=\frac{Eo}{Ru}+\frac{Eo}{Rv}+\frac{Eo}{Rw}$$
$$\frac{Eu}{Ru}+\frac{Ev}{Rv}+\frac{Ew}{Rw}=Eo(\frac{1}{Ru}+\frac{1}{Rv}+\frac{1}{Rw})$$
$$Eo=\frac{\frac{Eu}{Ru}+\frac{Ev}{Rv}+\frac{Ew}{Rw}}{(\frac{1}{Ru}+\frac{1}{Rv}+\frac{1}{Rw})}$$
Eu，Ev，Ewは三相電源であることから，Euを位相の基準とすると以下の通り表すことが出来る。
$$Eu=\frac{200}{\sqrt{3}}∠0°=\frac{200}{\sqrt{3}}$$
$$Ev=\frac{200}{\sqrt{3}}∠-120°=\frac{200}{\sqrt{3}}(-\frac{1}{2}-j\frac{\sqrt{3}}{2})$$
$$Ew=\frac{200}{\sqrt{3}}∠-240°=\frac{200}{\sqrt{3}}(-\frac{1}{2}+j\frac{\sqrt{3}}{2})$$
各変数に値を代入するとEo，Iu，Iv，Iwは次の通り求められる。
$$Eo=\frac{200}{9950\sqrt{3}}(2525-j825\sqrt{3})$$
$$Iu=\frac{\frac{200}{\sqrt{3}}-\frac{200}{9950\sqrt{3}}(2525-j825\sqrt{3})}{Ru}=2.656$$
$$Iv=\frac{\frac{200}{\sqrt{3}}(-\frac{1}{2}-j\frac{\sqrt{3}}{2})-\frac{200}{9950\sqrt{3}}(2525-j825\sqrt{3})}{Rv}=2.405$$
$$Iw=\frac{\frac{200}{\sqrt{3}}(-\frac{1}{2}+j\frac{\sqrt{3}}{2})-\frac{200}{9950\sqrt{3}}(2525-j825\sqrt{3})}{Rw}=1.446$$
各相に流れる電流と抵抗値から消費電力が次の通り求められる。
$$Iu^2Ru+Iv^2Rv+Iw^2Rw=733[W]$$
単純に電力積み上げした計算結果である733[W]と等しいことから，不平衡負荷においても単純に電力積み上げすることで問題ないことが分かる。
結論
三相電源に不平衡負荷を接続したモデルケースにて負荷電力を単純に合計して求めた消費電力と三相不平衡負荷の回路計算で求めた電力消費量が同一であることを示した。
よって，三相不平衡負荷においても電力量を求めるには接続する各負荷の電力量を単純に合計して良いことを確認した。
参考文献
日本電気技術者協会_理論計算の落とし穴(7)不平衡三相負荷の計算