【電験三種】誘導電動機の損失及び出力に関する問題_2021年7月新電気 電験三種予想問題 機械問3
目的
本記事では誘導電動機に対する理解を確認するための良問を紹介すると共にその問題の解法を示す。
誘導電動機に対する理解を確認するための良問
この問題は2021年7月に発売された新電気の電験三種予想問題 科目：機械 問3である。シンプルな問題文でありながら，誘導電動機に対する自分の理解を確認するのに適切な良問なので紹介する。
定格出力120kW，定格電圧6600V，周波数50Hz，6極の3相かご形誘導電動機がある。全負荷時の二次銅損は2kW，機械損は3kWである。この電動機の全負荷時の回転速度の値[min-1]を答えよ。
ただし，定格出力は定格負荷時の機械出力から機械損を差し引いたものに等しいとする。
解く上で必要な知識
・誘導電動機の等価回路の描き方
・等価回路の各素子で消費されるエネルギーの意味
実際に問題を解いてみる
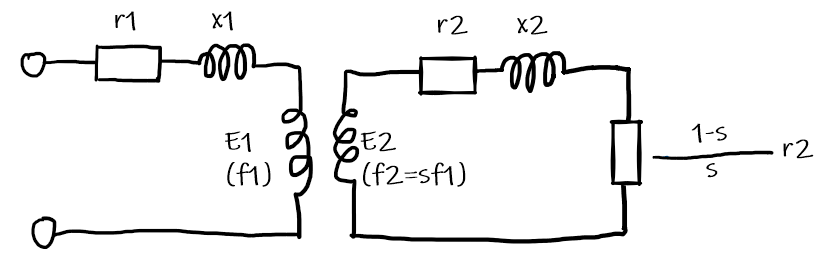
- まず，誘導電動機の等価回路を描く。
等価回路の描き方は以前投稿した記事にて紹介しているので興味のある方はご覧ください。
三相誘導電動機の出力式を導出する（電験3種平成30年機械問3)
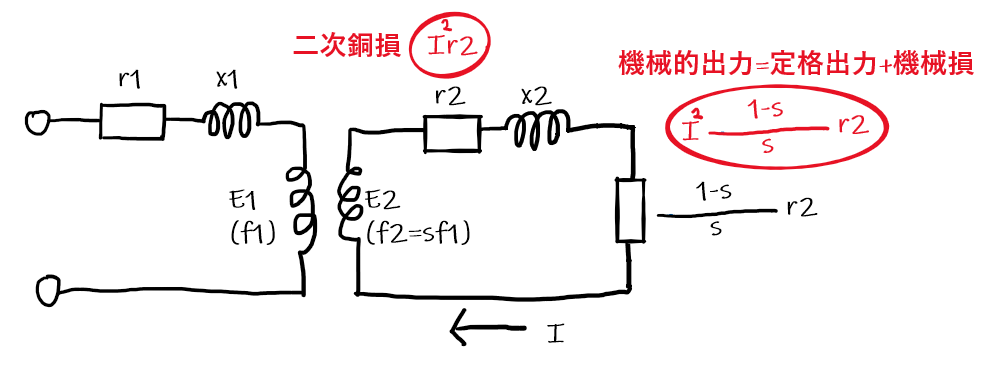
2. 二次回路に流れる電流をIとした際，各素子で消費されるエネルギーの数式とその意味は下図の通りとなる。
3. 問題文の数値を数式に当てはめると以下の通りとなる。回路は単相回路であるため，出力は1/3になることに注意が必要である。また，機械的出力は誘導電動機の軸出力及び機械損の合計であることに注意する。
$$I^{2}r_{2}\left( \frac{1}{s}-1\right) =\left( 120+3\right) \times 10^{3}\times \frac{1}{3}$$
$$I^{2}r_{2}=\left( 2\times 10^{3}\right) \times \frac{1}{3}$$
4. 上述の数式を展開すると滑りsが求められる。
s=0.016
5. 電源電圧の周波数が50Hzであることから，6極の誘導電動機の同期速度は1000[min-1]となる。
6. 同期速度に対して(1-s)を乗ずることで，誘導電動機の定格出力における回転速度が得られる。
1000 x (1-0.016) = 984 [min-1]